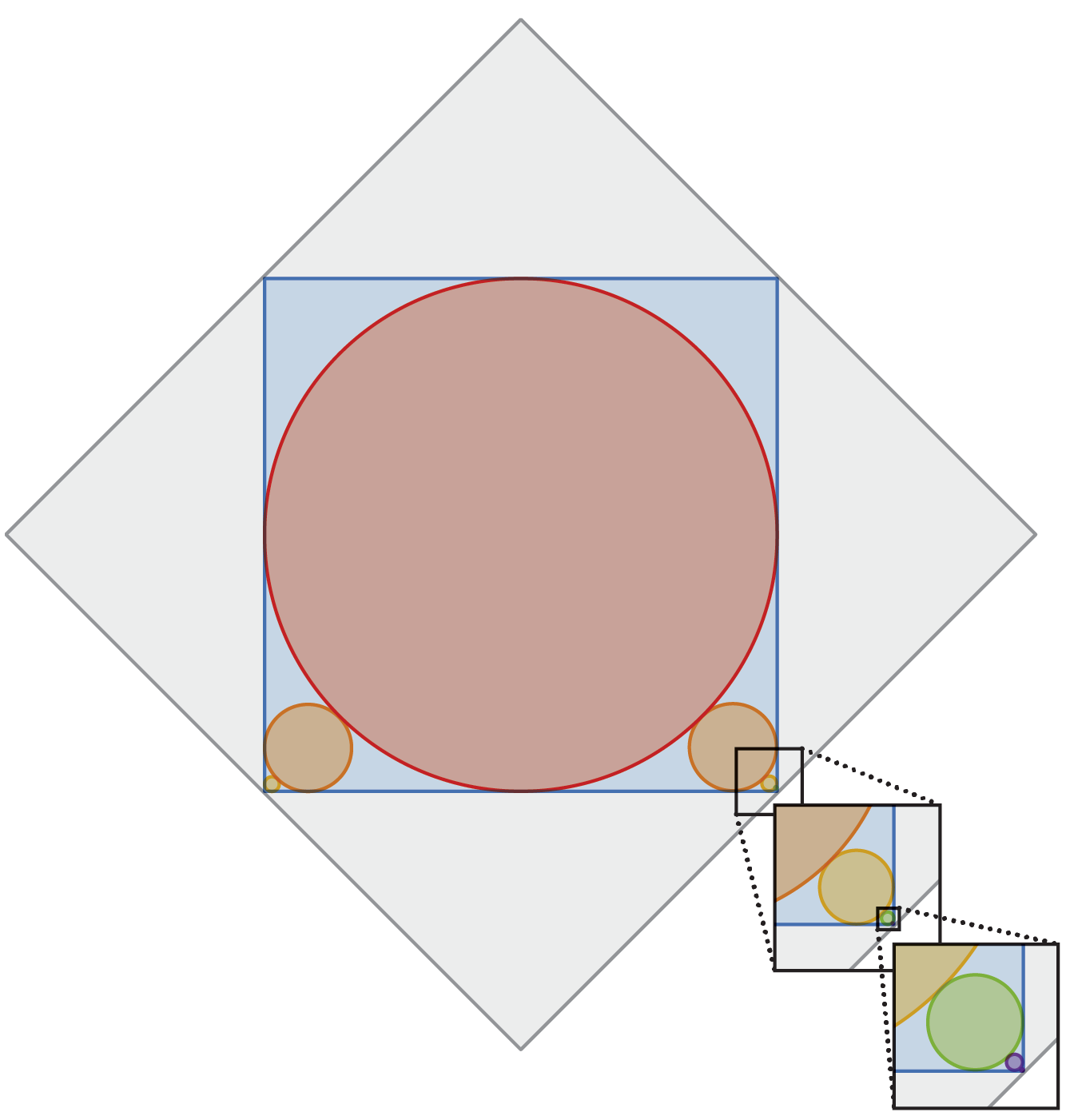
"A red circle is inscribed inside a blue square. The arrangement leaves gaps in the square's four corners, two of which are filled with smaller circles that just barely touch the big red circle and the two corner sides of the blue square. This, in turn, leaves two smaller gaps in the corners, which are filled with smaller circles, and so on, with ever smaller circles ad infinitum."
"The circumference of a circle is times its diameter. So the total circumference of many circles with diameters d1, d2, d3,... is: d1 + d2 + d3 + ... = (d1 + d2 + d3 + ...) So if we can find the sum of all the diameters, we can multiply that value by , and we're done. Because of the symmetry, the sizes of the circles don't change if we move some to different corners:"
A large red circle is inscribed in a blue square, leaving four corner gaps. Two opposite corner gaps are filled by smaller circles tangent to the large circle and to the two sides of their corner. Each filling creates two smaller corner gaps that are filled by even smaller tangent circles, and this process repeats infinitely. The circles' diameters form a decreasing infinite sequence whose sum equals the length of the blue square's diagonal. The diagonal equals 1 because the outer gray square has side length 1. Multiplying the total diameter sum by π yields the total circumference, π.
Read at www.scientificamerican.com
Unable to calculate read time
Collection
[
|
...
]